OSAA Rankings Frequently Asked Questions
General Ranking System Questions
1. What are the OSAA rankings used for?
OSAA rankings are used to help create contest match-ups for the first round of championship brackets once the playoff qualifying teams are known and to select teams in certain activities at some classifications. Additional rounds use rankings to determine home or away designation.
2. What sports are being ranked by the OSAA?
The OSAA is ranking schools in the following team sports: football, volleyball, boys soccer, girls soccer, boys basketball, girls basketball, baseball, and softball.
3. What system is the OSAA using for its rankings?
The OSAA is using a combination of a Rating Percentage Index (RPI) system and the Colley Bias Free Rating Method (Colley) for its rankings. The two systems generate a list of ranks that are averaged to create a team's overall OSAA ranking. In the event of a conflicting tie, the team with the higher Colley ranking will receive the higher OSAA ranking.
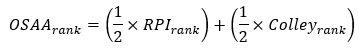
4. How is the overall OSAA ranking averaged: rankings or ratings?
A team's overall OSAA rank is determined by an equally-weighted average of their RPI and Colley ranking (see #3 above). In the event of a tie of this average, the better ranked Colley team is ranked above other tied teams. This overall rank is not calculated from component ratings of the two separate ratings systems. Ratings are only used for a relative comparison within the same system to determine the placement (rank) of teams within that system.
Ratings come from two separate and disparate systems whose values are not normalized across systems. Both systems generate ratings that fall within the set of rational numbers, but their ranges are different. The RPI ratings are a percentage index with values ranging from 0 (never won a game) to 1 (undefeated). RPI ratings represent an indexed value of a team's performance against their strength of schedule. The range for Colley ratings varies; they can be 0 to 1, the low end could be below 0, or the high end can be greater than 1 (depending on the variables). Colley ratings reflect the fitting coefficients to solve a system of linear equations to approximate a team's performance against all other teams.
Rankings are the numerical order of teams based on their ratings within their respective system (RPI or Colley). Rankings are in the set of non-zero, natural numbers (e.g., 1, 2, 3, ..., N) where #1 is the best-ranked team out of N total teams.
5. How are contests vs. out-of-state teams counted?
Results from contests against out-of-state teams shall be included in the RPI calculation. A team's Weighted Winning Percentage (WWP) and Opponents' Winning Percentage (OWP) will reflect any out-of-state opponents. Out-of-state contests are not counted in the Colley rating. Only contests against Oregon schools within the same classification and ±1 classification away are counted in the Colley ratings.
Schools are required to track the winning percentage of out-of-state opponents by updating their out-of-state opponent's win/loss record weekly. Schools are strongly encouraged to utilize the Out-of-State Opponents Form in order to have direct, regular contact with these teams. Schools must update their out-of-state opponents' records weekly (excluding any contest played against that particular school when counting wins, losses, or ties).
Out-of-state opponent's record are modified by excluding the contest(s) against the Oregon team. These modified out-of-state records do not include any forfeited contests by the out-of-state opponent. Out-of-state records should include regular season results and any league/district playoffs. State playoff results are not included.
6. Are the records of teams scheduled in the future included in the rankings?
No. An opponent is included in the rankings calculations only after the contest is played, not before.
7. Is the record used for an opponent their record at the time the contest is played or at the time the rankings are calculated?
Both RPI and Colley ratings are always calculated based on current records, not date-of-contest records.
8. How soon at the start of the season will rankings appear on the website?
Rankings will be available on the website beginning with the first contest date of each sports season.
9. Are the rankings updated in real-time once a team submits a result?
No, the rankings are set to update hourly. It would be great to have them in real-time, but the sheer number of computations being done takes too long.
10. The ratings only show out to 3 decimal places, is that enough precision?
The database which holds team rankings stores RPI and Colley ratings with a precision of 16 digits with a 15 digit decimal place scale - DECIMAL(16,15). This means that a rating can be stored as a fractional number with 15 digits after the decimal point (i.e. 0.971186815123126). Each rating number is represented with 11 bytes in the database per MySQL DECIMAL Data Type Characteristics.
On our website, decimal ratings are multiplied by 1000 and rounded to 3 decimal places (i.e. 971.187). This is to save space and make the numbers easier to read. This is only for display purposes. The system still uses the 16 digit precision for calculations. The architecture of the database and the web server code is setup to handle up to 16 digit floating point numbers, see the PHP Floating Point Numbers Documentation for more information.
When comparing two ratings, because of the nature of converting a base 10 number to base 2, there can be some precision lost. To compensate, an epsilon error is acceptable for decimal equality. The system uses an epsilon error value of 1E-14 (or 0.00000000000001).
11. How often will the ranking system be evaluated by the OSAA?
The OSAA Rankings Committee is a standing committee and reviews the ranking system including, but not limited to, the type of systems utilized, results to be included, home/away designation, rankings timelines, breaking ties, and placement of teams on state championship brackets. The committee forwards recommendations for modifications to the OSAA Executive Board.
The committee consists of four representatives of the Oregon Athletic Directors Association (OADA), four representatives of the Oregon Athletic Coaches Association (OACA) and one representative of the OSAA Executive Board. Members of the committee serve three-year, non-consecutive terms. Attention is paid to the term limit rotation to ensure balance between experienced members and new members.
The committee adopts an annual schedule of meetings based upon the issues under consideration. The schedule includes an appropriate number of meetings in which to conduct the business of the committee, typically three times each school year.
12. Why are the rankings on the OSAA website different than what I see on other websites or in my newspaper?
The official OSAA rankings are listed on the OSAA website. The OSAA has no control over what rankings are being displayed by other websites or newspapers. Rankings information is available via the OSAA API.
13. Do the OSAA rankings take into account where teams finished in state last year?
No, the OSAA rankings start from scratch each year.
14. Do the OSAA rankings factor in coaches' or media polls?
No, there are no coaches' or media polls of any kind included in the OSAA ranking system.
Specific Team Rankings Questions
15. Why do the rankings look weird early in the season?
The OSAA rankings system is a combination of two rankings systems: RPI and Colley. The RPI rating is primarily a measurement of strength of schedule and how a team does against that schedule. The Colley rating is a measurement of teams' success rates marked against opponents within the same classification and ±1 classification away.
There are no pre-season expectations or polls included. Every team starts from scratch each season. Consequently, the numbers can be skewed early in the season because teams have played so few contests or have not competed in a rankable contest. The data begins to take shape as more contests are played. The more contests that are played, the better the data gets.
16. Why doesn't my team appear in the rankings?
A team will not appear on the rankings until they have completed a rankable contest. For example, a team may play a JV team in the first contest or take part in a pre-season jamboree, both of which are not counted in the rankings, and would therefore have an incalculable ranking. Also, only contests that have a score can be considered. Schools are required by rule to input scores by 10:00pm the day of a contest. Sometimes, those scores are missing and were not counted in the latest rankings calculation.
17. Why is my team ranked behind another team that we beat?
The OSAA ranking system is a combination of measurements of a team's strength of schedule, how well a team does against that schedule, and the impacts of the team's opponents in addition to the team's overall performance in a season. To look at only one contest ignores the "any given day" aspect of sports. Only looking at a team's individual performance against a single opponent is too simplistic and narrowly focused to provide a fair, unbiased rating which compares every team to every other team.
18. My team bested an opponent by a considerably large margin, shouldn't that count as more of a win than just winning by a slight point differential?
No. Score differentials are not factored into rankings. Scores are not even used except to determine which team won, lost, or tied. A win is a win, no matter if it was a "blow out" or a "nail biter." Score margins do not matter at all in determining rankings. While a large victory margin may influence opinion, it does not influence the non-biased calculations. The object of a sport contest is to compete and exemplify sportsmanship. Wining a game is the objective, not winning by a large margin or running up a score.
19. Why did my team move up after a loss (or down after a win)? Why did my team move up (or down) when they didn't even play?
There could be several reasons. One is that since RPI factors in strength of schedule, it is possible to have a higher RPI after playing a good team, win or lose. Also, a team could move up or down by playing a "weaker" team, win or lose. A team's RPI rating or Colley rating can also change when they don't even play if one of the teams on their schedule or within their classification or neighboring classification has played. Keep in mind that these rankings are relative, meaning that a team's ranking is affected by the results of teams around them in the rankings. Colley ratings are even further reaching because they are impacted by all contests within the same classification and ±1 classification away (both immediately higher and lower classifications).
20. Why does my team's league record look wrong?
Although teams are placed into leagues (or special districts), the schools in those leagues determine which contests on a schedule count towards league records. Some larger leagues sub-divide their league into smaller "sub-leagues" and only count contests against certain opponents as league contests. Other leagues might choose to count multiple league match ups against the same league opponent only once. League procedures vary depending on the league and schools, and ultimately it is the school's responsibility to ensure their team schedules are entered correctly - including if a contests is a league or non-league contest.
21. How does my team have a league record when there are no completed league contests on their schedule?
There is a unique oddity that sometimes appears early in the season where a team will have a league record, but only has non-league contests on their schedule. This happens because schools mark a contest as a league contest by mistake (see #20 above). Whenever a league contest is scored, a team's league record is updated. However, school's do not catch the error of the contest being marked as a league contest and submit the score anyway. If a league contest that has been scored is later changed to a non-league type of contest, then a score does not have to be re-entered and any record or rankings impacts are automatically updated on the back-end. However, if a team does not have any scored league contests on their schedule, then their league record is not updated. The database was implemented as such to optimize the efficiency of the back-end calculation and generation of team records: why calculate a league record if there are no league contests to count? These oddities of "orphaned" league records are eventually updated once a team has a scored league contest on their schedule. Since records are not calculated using static accumulation, but rather a sum of scored league wins and losses from the overall team schedule data available at the time of calculation, this glitch is resolved once league play begins.
Rating Percentage Index Rankings Questions
22. What is the RPI formula?
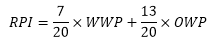 A team's RPI is calculated using a basic formula which includes two weighted variables. The first variable is a team's Weighted Winning
Percentage (WWP) which is multiplied by 35%. Wins and potentials are weighted depending on the contest location. The second variable is the team's Opponents' Winning Percentage (OWP) which is weighted at 65%. This is commonly referred to as the team's strength of schedule. Factors included are wins, losses, ties, and the location of the contest (home, neutral, or away). Score differential, coaches/media polls, and rewards/penalties for playing teams outside one's classification are not a part of the OSAA's RPI system.
A team's RPI is calculated using a basic formula which includes two weighted variables. The first variable is a team's Weighted Winning
Percentage (WWP) which is multiplied by 35%. Wins and potentials are weighted depending on the contest location. The second variable is the team's Opponents' Winning Percentage (OWP) which is weighted at 65%. This is commonly referred to as the team's strength of schedule. Factors included are wins, losses, ties, and the location of the contest (home, neutral, or away). Score differential, coaches/media polls, and rewards/penalties for playing teams outside one's classification are not a part of the OSAA's RPI system.
23. Are all contests included in the RPI rankings?
Wins, losses, and ties are included for all team sports including: endowment contests, contests versus independent status teams, and forfeits. Volleyball pool play matches from tournaments are not included. Cross level contests (i.e. varsity versus sub-varsity), contests versus alumni teams, jamborees, and cancellations are not included. Results from contests between 11-player vs. 8-player, 11-player vs. 6-player, 9-player vs. 6-player and 8-player vs. 6-player football teams shall not be included.
24. How are forfeits counted in the RPI rankings?
Forfeits count as a loss for the forfeiting team and a win for the team receiving the forfeit victory. League contests that are not played are counted as forfeits. Additionally, a team's OWP has any forfeits removed from that opponent's record unless the forfeited contest was played and the outcome on the field was not changed by the forfeit. For example, when a contest is forfeited by a team that lost and the contest was actually played to completion, then that contest is counted normally, as if the forfeit never occurred.
25. What happened to factoring in my Opponents' Opponents' Winning Percentage (OOWP)?
The RPI calculation only factors in a team's Weighted Winning Percentage (WWP) and Opponent's Winning Percentage (OWP). The third component of the standard RPI calculation, Opponents' Opponents' Winning Percentage (OOWP), was dropped effective beginning in the 2013-14 season. The PRI calculation was adjusted to reflect a more equal treatment of teams that play out-of-state opponents where OOWP records are virtually unobtainable for non-OSAA teams. Not factoring OOWP treats all OSAA teams equally regardless of their opponents. Analysis of OOWP showed little effect on RPI ratings so the weight of WWP and OWP was adjusted to account for the dropped effects of an average OOWP. Additionally, the symbolic equivalent of an OOWP factor is present and accounted for to a more complex degree in the Colley ratings system.
26. Why does a team's strength of schedule have a larger weight on its RPI than the team's winning percentage?
At first glance, it appears that the 35% and 65% percentages are focusing more on a team's schedule than winning percentage. However, in effect, more than half of the RPI rating is based on winning percentage. Although Weighted Winning Percentage (WWP) only receives a 35% weighting, its real impact on a team's RPI is larger. This is because there is always a wider gap in the ratings between the top and bottom teams in Weighted Winning Percentages (WWP) than between the top and bottom teams in Opponents' Winning Percentage (OWP).
Looking at the teams one at a time, the winning percentages can range from undefeated (1.0) to no wins (0.0). Even though the Weighted Winning Percentage (WWP) variable receives 35% weighting toward the overall RPI rating, its range of 1.0 (0 to 1) has a greater impact than Opponents' Winning Percentage (OWP). The range of all of the teams averaged, including all other opponents, usually doesn't vary that much. This is because the sample size is larger for the Opponents' Winning Percentage (OWP). Nearly all of the teams are going to have some wins and some losses, so the highest value is usually less than 1.0 and the lowest value is usually higher than 0.0. The range of Opponents' Winning Percentages (OWP) is therefore almost always smaller than 1.0 (e.g. 0.45 with values from 0.3 to 0.75). This means that the system has an effective impact higher than 50% for Weighted Winning Percentage (WWP) and lower than 50% for Opponents' Winning Percentage (OWP) because of the different range potentials for each variable.
27. What is the effective impact of a team's strength of schedule on its RPI?
The effective impact of a team's Weighted Winning Percentage (WWP) and Opponent's Winning Percentage (OWP) on its RPI is a representation of how much that team's Weighted Winning Percentage (WWP) and Opponent's Winning Percentage (OWP) actually affected the calculation of its RPI. As stated earlier, Weighted Winning Percentage (WWP) is weighted 35% and Opponent's Winning Percentage (OWP) is weighted 65%. However, the effective impacts can be calculated once the season is complete (i.e. after rankings have been frozen). The equation to find the effective impact of a team's strength of schedule is below.
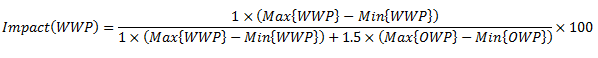
The first step is to find the range of every Weighted Winning Percentage (WWP) and Opponent's Winning Percentage (OWP) within the same classification. The range of Weighted Winning Percentages (WWP), for instance, is calculated by taking the maximum value of the set of Weighted Winning Percentages (WWP) and subtracting the minimum of that set. (For statistical purposes, teams that competed in less than 5 rankable contests are excluded from these sets because of their negligible impact.) These ranges are multiplied by their weight from a normalized WWP:OWP ratio of 1:13/7, which comes from the 35% and 65% weights normalized for a team's strength of schedule. The weighted range over the total weight gives the actual effect, or effective impact, that a team's strength of scheduled had on its RPI.
28. What is a team's Weighted Winning Percentage (WWP)?
The weight of a particular contest is determined by its location.
| Home Win = 0.8 of 0.8 | Away Win = 1.2 of 1.2 | Neutral Site Win = 1.0 of 1.0 |
| Home Tie = 0.4 of 0.8 | Away Tie = 0.6 of 1.2 | Neutral Site Tie = 0.5 of 1.0 |
| Home Loss = 0.0 of 1.2 | Away Loss = 0.0 of 0.8 | Neutral Site Loss = 0.0 of 1.0 |
For example, a team that has a win-loss record of 3-0 at home and 1-4 on the road has a weighted record of 3.6 wins (0.8 × 3 home wins + 1.2 × 1 road win) 3.2 losses (0.8 × 4 road losses). Even though the team's overall win-loss record is 4-4, their weighted win-loss record is 3.6-3.2. For RPI purposes, their Weighted Winning Percentage (WWP) would then be .529 (3.6 ÷ 6.8) as opposed to a non-weighted percentage of .500 (4 ÷ 8).
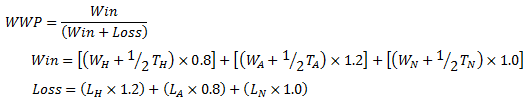
This weighted record is used for the 35% of the RPI formula as each team's Weighted Winning Percentage (WWP). The regular, non-weighted team records (wins and losses) are used to calculate a team's Opponents' Winning Percentage (OWP).
29. If a team plays an opponent more than once, is their winning percentage included more than once?
Yes, it is included once for each time a team plays that opponent and all contests against the team in question are removed from each occurrence of that opponent's record when calculating Opponents' Winning Percentage (OWP).
30. Is the Opponents' Winning Percentage (OWP) adjusted to account for the fact that they have played the team in question?
Yes, all contests against a particular team in question are ignored when calculating that team's Opponents' Winning Percentage (OWP).
31. How is a team's Opponent's Winning Percentage (OWP) calculated?
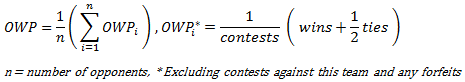 A team's Opponent's Winning Percentage (OWP) is calculated by taking each opponent's adjusted record and converting it to a non-weighted winning percentage. All of those opponent's winning percentages are then averaged, dividing their sum by the number of opponents. Opponent's Winning Percentage (OWP) records are adjusted to not include contests against the team for which the Opponent's Winning Percentage (OWP) is being calculated for. Any contest that had been won or lost due to a forfeit is also excluded from Opponent's Winning Percentage (OWP), unless that forfeited contest was played to completion and the team that lost was the team that forfeited (i.e. the forfeit did not change the outcome of the contest).
A team's Opponent's Winning Percentage (OWP) is calculated by taking each opponent's adjusted record and converting it to a non-weighted winning percentage. All of those opponent's winning percentages are then averaged, dividing their sum by the number of opponents. Opponent's Winning Percentage (OWP) records are adjusted to not include contests against the team for which the Opponent's Winning Percentage (OWP) is being calculated for. Any contest that had been won or lost due to a forfeit is also excluded from Opponent's Winning Percentage (OWP), unless that forfeited contest was played to completion and the team that lost was the team that forfeited (i.e. the forfeit did not change the outcome of the contest).
32. How are ties counted in the RPI rankings?
Ties are counted as half the weight of a win for that team based on the location of the contest. An away team would receive 0.6 out of 1.2 for a tie, while the home team would receive 0.4 out of 0.8 for a tie. Ties at neutral locations are worth 0.5 out of 1.0 for both teams. When calculating Opponent Winning Percentage (OWP), all contests are weighted as 1.0, regardless of designation or location played.
33. How do schools determine home/away designation for a contest?
Since the RPI system factors in where a contest is played, it is important that schools correctly designate this information when entering schedules and reporting results, especially for double-headers and tournaments. Teams may be considered to be playing a home contest even if the contest isn't played on the schools' campus (e.g. Century High School playing football at Hillsboro Stadium is a home contest for Century). Tournament play shall be considered a neutral site, except for contests played by the tournament host at its home venue. Baseball and softball contests, even those played as part of a tournament, shall not be listed as neutral due to the fundamental difference associated with being the home team in those sports (advantage of batting last).
Colley Rankings Questions
34. What are Colley ratings?
The Colley Bias Free Rating Method was developed by Wesley Colley, Ph.D. and is based on winning percentages. Those percentages are adjusted for a team's strength of schedule. Only contests against opponents within the same classification and ±1 classification away (both immediately higher and lower classifications) are included in the calculation formula. When this system is expanded to include all teams in a classification and ±1 away, a linear system of equations is created with the same number of variables as there are teams within the considered classifications.
This massive system of equations is solved using an augmented matrix filled with teams' contest counts and countable records. The resulting solutions for the matrix are ratings for each team in the classification that measure the team's winning percentage against the strength of its opponents and the interactions of their opponents with all other teams within the same classification and ±1 classification away. This method effectively removes the effects of "padded" schedules and factors each team's performance compared to every other team within the same classification and ±1 classification away.
35. What contests are counted in the Colley Rating?
If a contest was to be normally included in the team's RPI calculation and the contest was between opponents within the same classification or ±1 classification away, then that contest will be counted in the Colley calculation. Contests versus out-of-state opponents are not included.
36. What is the Colley calculation?
The Colley method of calculating team ratings is basically done by using a matrix to solve a massive system of linear equations. A matrix, M, is filled with a count of contests each team has played against every other team in the same classification and ±1 classification away. A right-hand-side vector of win, loss, and tie records, B, is the solution of the matrix M multiplied by a ratings vector X.
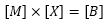
37. What factors are calculated in the Colley matrix equations?
The Colley method uses two matrices (M and B) to find the solution of a third matrix (X). The first matrix, M, is a square matrix the same size as the number of teams in consideration within the same classification and ±1 classification away. Each entry in matrix M that is not on the diagonal is a representation of the number of times team i has competed against team j multiplied by -1. The equation for non-diagonal entries in M is:

In M, the diagonal entries represent the total number of contests that team i has completed, plus 2 to assume every team starts out as an average team (one win and one loss). This assumption is important in defining the nature of the matrix. The equation for diagonal entries is:
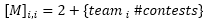
The matrix B is a one-dimensional vector array filled with each team's record calculated by the equation:
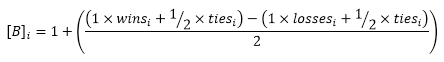
The solution vector X holds a ratings value for each team that solves the system.
38. How is the Colley matrix equation solved?
The matrix X which holds each team's Colley rating is calculated by solving the system of linear equations in the matrix equations by preforming a Cholesky Decomposition and then preforming a forward and backward substitution. The assumption that each team starts off as average with one win and one loss is essential by ensuring the matrix M is symmetric and positive. The nature of such a matrix is that its decomposed lower-triangular matrix multiplied by its mirrored upper-triangular matrix is itself. This allows a quick calculation to be done instead of preforming a lengthy and costly matrix inversion.
For example, consider a case with 5 teams: A, B, C, D, and E.
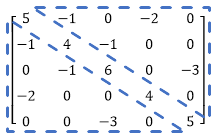
Team A played against Team B once and against Team D twice. Winning all three of its games, Team A's record is 3-0. Team B lost to Team A once, and won once against Team C for a record of 1-1. Team C lost against Team B and played Team E three times. Of the three times Team C faced Team E, Team C won once and lost twice. Team C's record is 1-3. Team D's record is 0-2 with the two losses to team A. Team E only played Team C, so its record is 2-1. The matrices M and B are calculated from these records and the system of equations can be expressed below:

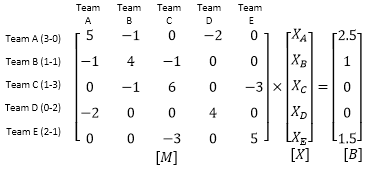
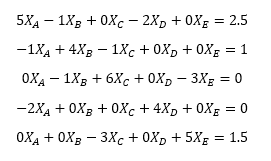
Note the matrix M is symmetric. Because of this property, the system can be decomposed into a lower-triangular matrix which can be easily used to solve the system. This is accomplished computationally to find the solution matrix X, which holds the ratings for teams A-E.
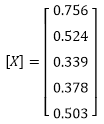
Therefore, from these ratings, the top Colley ranked team is Team A (3-0) with a rating of 0.756, second is Team B (1-1) with a rating of 0.524, third is Team E (2-1) with a rating of 0.503, fourth is Team D (0-2) with a rating of 0.378, and last is Team C (1-3) with a rating of 0.339.
To easily check these numbers and to solve the system, use a calculator to setup the two matrices M (5x5) and B (5x1) with the example's numbers. Solve 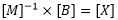 .
.
Playoffs and Brackets Questions
39. Are the rankings being used to select which teams qualify for the OSAA State Championships?
Yes, but only in certain activities at some classifications. Refer to that sport's playoff qualifications page for more details.
40. At what point in the season will the OSAA use the rankings to match up teams that qualified for playoffs?
The rankings for each team sport shall be available to the public via the OSAA website beginning with the first contest date of each sports season. Rankings for all classifications in each team sport shall be frozen at 10:00 PM on the following dates, including all contests played that day:
| 2022-23 Rankings Freeze Dates | 6A | 5A | 4A | 3A | 2A | 1A |
|---|---|---|---|---|---|---|
| Football | Sat, Oct. 29 | Sat, Oct. 29 | Sat, Oct. 29 | Sat, Oct. 29 | Sat, Oct. 29 | Sat, Oct. 29 |
| Volleyball | Sat, Oct. 22 | Tues, Oct. 25 | Thurs, Oct. 20 | Sat, Oct. 22 | Tues, Oct. 25 | Sat, Oct. 22 |
| Soccer | Tues, Oct. 25 | Sat, Oct. 29 | Tues, Oct. 25 | Tues, Oct. 25 | Tues, Oct. 25 | Tues, Oct. 25 |
| Girls Basketball | Fri, Feb. 24 | Tues, Feb. 28 | Tues, Feb. 21 | Sat, Feb. 18 | Sat, Feb. 18 | Sat, Feb. 18 |
| Boys Basketball | Sat, Feb. 25 | Wed, Mar. 1 | Tues, Feb. 21 | Sat, Feb. 18 | Sat, Feb. 18 | Sat, Feb. 18 |
| Baseball | Thurs, May 18 | Sat, May 20 | Mon, May 15 | Thurs, May 18 | Thurs, May 18 | Thurs, May 18 |
| Softball | Thurs, May 18 | Sat, May 20 | Mon, May 15 | Thurs, May 18 | Thurs, May 18 | Thurs, May 18 |
41. Do league champions receive home games in the first round of the state playoffs?
League champions at the 5A, 4A, 3A and 2A classifications shall be guaranteed a home game in their first state playoff contest, provided that the league champion finished in the top 16 of the final frozen rankings. League champions at the 6A and 1A classifications shall be guaranteed a home game in their first state playoff contest in 32-team brackets regardless of final frozen ranking. In 1A-8 player football, league champions must be in the top 12 of the final frozen rankings to receive a home game in their first state playoff contest. In 1A-6 player football, league champions must be in the top eight of the final frozen rankings to receive a home game in their first state playoff contest. In 6A football, league champions in the top 16 of the final frozen rankings will receive a home game in their first state playoff contest. League champions outside the top 16 in 6A football will be moved into the top 16 but will not be guaranteed a home game.
42. How is the home/away designation figured for playoff games?
According to the Board Policy "Home Team Designation" which was revised effective beginning the 2013-14 school year, during all rounds of each OSAA State Championship bracket, the better seeded team shall be the designated home team. Teams are not re-ranked nor re-seeded after initial placement on the bracket.



